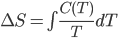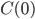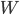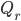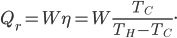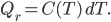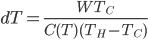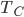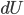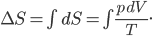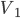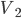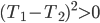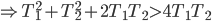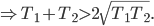Fantasy isn't my favorite genre. It's nearly always set in some vaguely medieval setting, but without Christianity (who can separate those?) and includes a ton of lore about magic, dragons, along with elves, dwarfs, and other variations on humanoids who have different British accents. The trappings take over, and not much compelling ever seems to happen. I always feel like I'm sitting in a seminar on magic spells and elven history.
In gaming this problem is particularly acute, since fantasy outings normally show up in the form of role-playing games with a "silent protagonist". This is another way of saying that the story has no main character, a concept which ought to be obsolete in narrative gaming (see, for instance, the inexplicably popular Skyrim). It could be that these games just aren't aimed at a general audience, but rather one that is obsessed with making the experience "their own", tailored in every possible way. (In a naked admission of this, the quite popular Demon Souls and Dark Souls are nearly totally gameplay with no real exposition whatsoever.)
After everyone's recent falling out with Mass Effect, I started hearing very good things about CD Projekt's The Witcher series. The developer seems to mock Mass Effect and other Bioware outings by stating that while there are decisions to be made, none of them is inherently moral or immoral (denoted by ME's "Paragon" and "Renegade" points, an unnecessary and trivializing gamification of choice). Encouraged by good reviews from Eurogamer and the recent Steam sale, I picked up both The Witcher and The Witcher 2: The Assassin of Kings.
The set up
Origin stories are sometimes a bit of an annoyance. Spiderman is weighed down by the need to introduce how Peter Parker gets his powers, and only in its sublime sequel do we commence with a real adventure: a battle with Doc Oc. The Witcher suffers somewhat for being an origin story, as the world is reckoned to be very foreign to the player. It's not quite pastiche; the universe has a strange mix of real science like genetics along with magic and alchemy. Geralt, the main character, and other witchers like him, are genetic experiments carried out by sorcerers, modified so that they are sterile but hardy as hell and with limited magical ability. One would think that the last sentence would be enough explanation to acclimate the player, but instead the story falls back on the protagonist-who-lost-his-memory trope, so that the universe can be explained in painstaking detail to the player.
We first see Geralt running from something, near death, but he is miraculously found by two of his fellow witchers and brought back to his former witcher enclave (which is a castle). He remembers nothing, and everyone else says that he had died some years earlier when a mob came to kill a group of nonhumans and lynched him. His ex, a sorceress named Triss, resides with the witchers. Geralt has no memory whatsoever of their relationship and why it ended, putting him in an awkward spot when she offers to sleep with him shortly after his arrival.
Right, so here it is: Geralt is basically James Bond in Middle Earth. He kills shit, he gets with the ladies (who know they don't have to worry about pregnancy with him), he is a tough guy with an occasional conscience, he pretends to be an instrument of powerful people, but in reality determines a lot of important events. All the misogyny that can be read into Ian Fleming's work can also be read here, possibly more so. Sleeping with women (I think you can bed something like 14 throughout the game) gets you collectible trading cards. I'm not kidding. So that's kind of horrible and trivializing of women, and it doesn't reflect well on the game.
Events are predictably propelled forward when the witcher fortress is attacked and its important powerful secrets are taken by persons unknown. Geralt and Triss split up to investigate leads as to who the perpetrators are, and the game soon becomes quite unfocused. You move from one setting to another encountering something like vignettes, a world rich with incredibly muddy morality. The writers seem to have sat down and made sure that every character had just as many traits to make them sympathetic as to make them unsympathetic. This is particularly apparent (and, I might add, effective) when deciding whether to side with nonhuman rebels, called Scoia'tael, who are fighting against oppression and for equal rights by some incredibly questionable methods (murder, theft, and terrorism). On the other side is a knightly order with a strict moral code that happens to include deeply held racism.
Choosing between these two sides is somewhat functionally substantial. Unlike Mass Effect, where the decisions are normally self-contained and scene-by-scene, in The Witcher once you choose a side events are going to play out differently, different tasks will be assigned, people you alienate will not talk to you, and some areas are unavailable.
The game as a whole is a mixed bag. In the Zero Punctuation review, Yahtzee says he played for 2 hours before giving up, and you can kind of see why. Built in the Neverwinter Nights engine and released in 2007, the game is clumsy and overly complicated, at least by today's standards. Combat is a boring exercise in timed clicking combined with switching between fast and slow attacks. Grinding for experience isn't too onerous, but it is here. There are a fair number of fetch quests and a whole shitload of running around. Waiting for a period of time or mixing potions can only be done at a lit fireplace. Character models are reused so often than it is incredibly distracting.
If one can get past these things, The Witcher has some good payoffs, especially near the end of the game. Geralt's former predicament remains obscure, but the setup for the story to continue is there, and the interaction between the witcher and his former lovers and friends is provocative. The game dovetails into Witcher 2 in a fairly substantial way, one that isn't apparent until nearly the end.
Getting to the Good Stuff
It's hard to say if one could play Witcher 2 without having played the previous game. It jumps headlong into the action, with no drawn-out explanation of how Geralt finds himself where he does. Having saved King Foltest from a mysterious assassin's sword some months earlier, the witcher is kept on as the king's lucky charm as he puts down an uprising within his borders. Needless to say from the subtitle The Assassin of Kings, things don't work out so well, as another mysterious murderer finishes the job the first could not. Geralt goes on the lam with Triss after gaining the trust of Foltest's elite soldier Vernon Roche, seeking to clear his name and find the people responsible for the death.
Whereas the first outing was meandering, this game is drastically more focused. While not having quite the linearity of Uncharted, the game doesn't explode into a huge number of meaningless side quests. Subplots, where they exist, are given weight and nearly always include characters with some depth. Gone are the numerous meaningless sexual escapades, and in their place far more organic and singular experiences (at most three sexual encounters in a single playthrough). And we start (and finish) to unravel Geralt's lost memory, a block that I thought was unneeded in the first place. The gameplay itself is much more like a third-person action game, and it feels just fine with either mouse/keyboard or gamepad (I preferred and Xbox controller). Finally, visually the game is a treat, with wonderfully made character models, settings, environmental and lighting effects in a very good game engine.
One of the amazing things about it is that Witcher 2 is practically two games in one, something I didn't initially note. I mentioned earlier that Geralt pairs up with Vernon Roche, but he does so after Roche had him imprisoned and beaten for several days. A short time into their adventure, a choice can be made to stick with Roche or split and join with the Scoia'tael leader Iorveth, as angry and dickish an elf as you're likely to meet. This choice can be rationalized either way. When I first played the game, I stayed with Roche, as he had let me out of jail, trusted that I wasn't the killer and was helping clear my name. Going back for a second playthrough, it was equally easy to side with Iorveth, as although he tried to kill me, he hadn't tortured me for several days in a dungeon.
It was during the second playthrough that I realized that nothing was the same. The plot of the second chapter isn't just told from a slightly different perspective or with one or two details changed---it consists of entirely different events and largely in a different setting. And both are interesting! Some of this divergence is retained in the third chapter, though the two paths join in most substantive ways by the end.
The writing is actually quite good. I don't know that I think the dialog is quite on the level of Uncharted, but Triss Merigold and Geralt are both well acted and believably written, as is the "villain" and many of the supporting cast. Triss is much more the focus of this game than the last, in terms of technical achievement (her naked body was on the cover of the Polish version of Playboy, and no I will not link to it from my site, but it clearly was the product of a lot of work) and character development. One moment early in the game where she teases Geralt about an ill-advised tattoo had me genuinely charmed. Seeing how this relationship stands up (supposing you want it to) in the face of Geralt's returning memory is intriguing, and I thought that could have used more screen time.
Witcher 2 feels like grown-up fantasy. It's got grit without feeling affected, it has honest moments without getting melodramatic, and it offers choices that both feel and are narratively substantial. The side quests are fun and interesting, there's no god damned grinding. It has charm, humor, and it's inventive. I loved every minute of both times I played it.