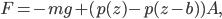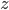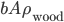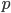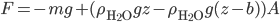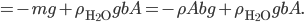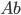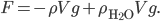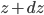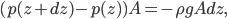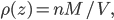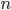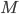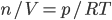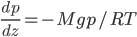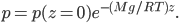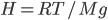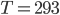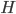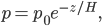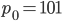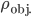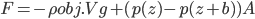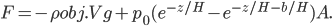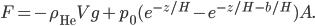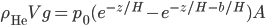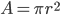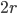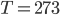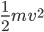Idle Analytics

Boats, hot air balloons, helium balloons: all of these things defy gravity. Gravity is pulling down on them, but they don't fall all the way to the ground. If you had a helium balloon on the moon, it would not rise: gravity would prevail and pull the balloon to the ground. That's what gravity does. So how is it that things float, and to what extent will they do so? Well, obviously it has something to do with them being in air or water. But why?

Let's start out with something a bit easier. When you swim to the bottom of a pool that's more than, say, 6 ft deep, your ears hurt because the pressure (hydrostatic pressure) is larger there than we're used to. Why is that? Because the water at the bottom of the pool has to hold up all the water that's above it. And water weighs a lot!

If you have glass, and you add a layer of water to it, the molecules in that layer are at a certain density. When you add a 2nd layer, the 1st layer gets crunched down a bit due to the weight of the water in the 2nd layer. It doesn't compress very much in terms of volume, but the pressure rises until it's holding the 2nd layer up. As you add more layers, the 1st layer gets squished more and more, and its pressure keeps going up. The pressure in the 2nd layer also goes up as it has to hold the 3rd, 4th, 5th layers up as well. Think of it like gymnasts forming a column, with each guy standing on a lower guy's shoulders. The more guys in the column, the more stress on the first guy.

This implies that there's a gradient of pressure: the lowest layer has the highest pressure, the highest layer has the lowest pressure, and there's a linear relationship between depth and pressure. The molecules at the bottom have to crash into the molecules above them harder in order to hold the weight up. The weight is 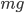, but it's better to express the mass as the density, mass divided by volume, times the volume. So the pressure is

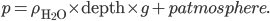
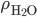is the density of water. That's simple, because the density of water doesn't depend very much on depth, and is therefore just a constant. So the pressure at 2 meters is 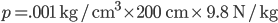which is 1.960 N/cm² or 19600 pascals more than at sea level. That's about a 20% increase, since normal atmospheric pressure is 101000 pascals. And your ears aren't really "designed" to handle that.

Now, some things float and some things sink in water. Things that are "lighter" than water float. Wood, ice, (apples, churches, very small rocks) and other things that are less dense float. We want to say why that is.

Let's just focus on a block of wood, submerged in water, that has a thickness 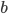and area 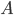. Its density is 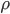. The pressure on the bottom of it is higher that the pressure on the top of it, for the simple reason stated above.

If the density 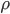is bigger than 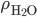, the object has a net force downward and therefore sinks. But if 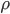is less than 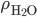, which for wood, it is, the object actually has a net force upward, and rises. Density is the determiner. The buoyant force, upwards, is 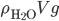, which is the weight of the water that would have been in that volume if the wood wasn't there. This is called Archimedes' principle, about which he supposedly screamed "Eureka"' and ran naked through the streets of Athens. If the buoyant force is greater than the weight, you have floating.

Now, the water at a certain depth is holding up the water above it, but it's also holding up the entire atmosphere above it too. That's why the pressure is 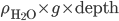more than atmosphere. At a depth of zero the pressure is regular atmospheric pressure 101 kPa. Things also have buoyancy in air. Helium balloons float because they are "lighter than air". But lighter than air means less dense.

Just as before, let's determine how pressure varies with height, but this time in the air. It will be a bit different physics this time, since the density of air is not constant with altitude. In fact, the air gets thinner as you go up.

Unlike for water, the ability to float in air depends upon elevation. Duh! Once you get high enough that there's no air, the air can't provide buoyancy.

For relatively low altitudes, the function 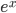looks almost exactly like 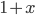, so this is approximately

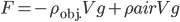
which is the same as Archimedes' principle; that is, the buoyant force in air is approximately equal to the weight of air displaced.

But for high altitudes, we can't make that assumption. So we can ask another question: when will a helium balloon stop floating? This is just meant to give us an idea, so it won't be totally accurate.

Then, the height that the balloon rises to is roughly 20 km or 12 miles. At that point, the weight of the object balances the weakened buoyant force, and in principle it will just stay there forever. But this inherently limits our ability to survey the Earth by balloon. We can probably never get to the outer layer of atmosphere, called the thermosphere, by use of a balloon. For that we have to use rockets to position satellites, since buoyancy peters out too fast as you go away from the ground.

Footnote: There are several technical problems with this final calculation. For very light material of the balloon, the pressure inside will expand the balloon as it goes up, due to the reduced pressure outside with constant pressure inside. The balloon will therefore pop before too long. On the other hand, if you used a hard material, it would be considerably heavier, and therefore you can't ignore the weight of the balloon itself. Real weather balloons can reach much higher than this (almost 100 miles), whereas a regular rubber balloon might only make it a few hundred feet before bursting.

Why is it that the cheesy part of a pizza can burn your mouth, but the crust doesn't? They both came out of the same oven, at the same temperature, but it seems like the cheese has more "heat" (actually internal energy ) stored inside of it. When you put it in your mouth, it heats your mouth until it and your mouth reach the same temperature. But while the crust seems to give up all its heat quickly, and without having to throw off very much heat, the cheese seems to throw off a ton of heat in order to reach your mouth's temperature.

Thermal internal energy , is the energy inside something that is in the kinetic and potential energy of the atoms that make it up. There must be some relationship between and the temperature . But what is that relationship? Is it the same for all substances? What do you think?

The heat capacity is the amount of heat you need to add to something in order to make the temperature increase by 1 degree. It takes 1 calorie to make 1 cubic centimeter of water rise by 1 Kelvin. (That's just the definition of a calorie.) For 1 cubic centimeter of air, the amount of heat you have to add to go up 1 Kelvin is only around 0.0004 calories. So water has more than 2500 times more heat capacity for the same volume! Metals like aluminum have a heat capacity somewhere in between water and air, at about 0.5 calories to make a cubic centimeter go up 1 degree.

Suppose the power goes out, and you're worried about the tiramisu you have in the refrigerator spoiling. If the fridge has nothing in it but your dessert and air, you have a problem. Heat will start leaking in, and will easily increase the temperature of the air. This heat will then all go directly into your dessert. But if you have a bunch of water bottles in there, all at low temperature, you're much safer. It will take a long while before the heat leaking in can appreciably increase the temperature of  the water.

What might be obvious from this discussion is that if you have a substance of some volume, the more particles you have in that volume the better, for storing heat anyway. Gases are diffuse, so 1 cubic centimeter (at standard pressure) isn't very many atoms. Water and metal are dense, so there's a lot of atoms per volume. This makes sense. If the temperature is the average energy per particle, then adding a fixed amount of heat (like 1 calorie) is going to give you varying amounts of temperature increase. For gas, the heat is divided among relatively few atoms, so each gets a large share and the temperature rises a lot. In dense materials the energy gets divided among lots of atoms, so there's a small temperature change, as each atom gets a small portion.

This is not to say that the heat capacities for all gases are the same. Some gases are better at stuffing heat into themselves than others. When a gas absorbs heat, since there is no potential energy between gas atoms, a given molecule has to put the heat into either kinetic energy, or potential energy within the molecule by the stretching of the chemical bond. But some gases have more kinds of kinetic energy than others. Moving along a certain direction is one way of having kinetic energy, but rotations and tumbling is another way. If a gas is monatomic, meaning that the atoms in the gas aren't bonded to each other, then the gas only has 3 ways of moving, one for each dimension it can travel along (, , and ). It can't tumble because it's just a point. This would include things like argon, neon, and xenon. But lots of gases, like the air, are made up of diatomic molecules, where the atoms pair up to make barbell shaped molecules (such as O₂ and N₂). These gases then have three extra ways of storing energy, and thus three extra ways to stuff energy into themselves: they can rotate along two axes, and they can put energy into stretching of the bond between them. As such, they have a higher capacity for holding heat. If that's so, then oxygen gas (which is diatomic) should have double the heat capacity of argon gas (which is monatomic). Is that true? Yes!

If we think of it that way, then all solids should have the same heat capacity. Solids have 6 ways to divide energy up, 3 kinetic and 3 potential. There's no tumbling nonsense like above, just a bunch of atoms held in a 3D crystal as if by little springs to each other. So, speaking of metals specifically (and almost all species on the periodic table are metals), they should all have the same heat capacity per particle (or per mole), and it should be roughly the same as air (per molecule! Not for the same volume, for the same number of molecules). And it's true! The heat capacities for most metals are about 6 calories per degree C for every mole, within 15% of air (6.9 calories per C per mole). This is called the law of Dulong and Petit.

Now, water is a whole other story. Unlike gases, it has potential energy. And unlike solids, it has tumbling in addition to this potential energy. And it has two molecular bonds to store energy in. So, water can store a ton of heat without going up in temperature very much. If you microwave a burrito, the plate can get very hot while the burrito is lukewarm. Why? Water! You put the same amount of heat into both the plate and the burrito, but the temperature of the plate went up much faster because it doesn't have as many ways to stuff heat into itself (i.e. it has a low heat capacity). The burrito, by having water in it, has tons of ways to store heat (i.e. it has a high heat capacity). So the temperature of the burrito goes up very little compared to the plate.

So, the first law is , where means the change in internal energy, is the heat, and is the work done. This is true whenever the thing we're paying attention to isn't losing or gaining particles, which we'll consider later.

Let's check our understanding. Consider an air canister, like those used to blow dust out of computers. The air that comes out of it is cold. Why? The First Law says that will go down (and hence temperature will go down) if either goes out or the system does work on something. Is there heat involved in letting the air out of the canister. No. Is the air doing work as it leaves? Yes! It has to push the air in front of it out of the way as it expands. That lowers its internal energy and its temperature. If you discharged that gas into a vacuum, the temperature would not go down.

But what about if you want to just use electricity and cycle something to make cold, such as your refrigerator and air conditioners do? There is no such thing as "cold". There's heat, which is the transfer of energy into something's internal energy. But there is no anti-heat. Burning something makes heat, but there's no simple way to make "cold". It's hard to see how you can build a closed-cycle refrigerator, where no atoms leave. (Try to think of how you would do that. I'll wait.) Here's an idea: will decrease ( will be negative) if we could find a way to let the system do some work without heating it ( but ). And if decreases, then temperature does too. That's the same as the air expanding from the air can. But we can also do this by use of a piston.

Here is the schematic way that almost all refrigerators and air conditioners work:

1. Start with some substance (gas) in a vessel that can control its volume (a piston).
2. Compress the gas. In doing so you will heat it up because you did work on it. (This is why the outside unit in your AC is called a compressor.)
3. Now let it come to equilibrium with the outside air by heat conduction. Heat will leave the gas, reducing its internal energy, and making its temperature roughly the same as the outside air's (this is why AC compressors have a big fan in them. It's also why the AC compressor has to be located outside: you don't want to dump that heat into your house. Otherwise you'll actually heat your house instead of cooling it!)
4. Since the pressure is now higher inside the piston than outside, let the piston expand. The gas will do some work, lowering its internal energy and hence its temperature. You have now made the gas in the piston cold. Place whatever it is you'd like to be cold (like a soda, or your house) in contact with the piston, which will absorb heat as long as its temperature is lower than what you want to cool down.

But is making our soda cold all that we've done? We made the soda cold, but what about the whole planet, or the universe? This I leave to another day, but note that we had to throw some heat into the atmosphere, and moreover somebody had to do some work from the outside to compress the gas in the first place.

Now, going back to the first example, we can make something cool by losing particles. Another type of in-home cooling is an evaporative cooler or a "swamp cooler".  This is an extremely simple device. You have a mesh that is coated in water, and you blow air through the mesh. The air that comes through is cooler than went in, though it is slightly moister. Why the heck does this work?

The first thing to realize is that the overall speed of the air is tiny compared to the speed of the molecules in it. It's sort of like carrying a box of gas to another location, in contact with water, and the carrying it away again. Some of the water evaporates into the air as it passes through. The vapor is at a relatively low temperature, since the molecules gave up their energy in the jumping out. The air is now mixed with a cooler water vapor, reducing the temperature.

An evaporative cooler won't work well if the air is already saturated with water. Lots of water in the air makes evaporation harder, since for every molecule that evaporates, another one that was already vapor condenses on the water. So you would never use a swamp cooler in a swamp! Dry environments work best. (Conventional wisdom is that the name "swamp cooler" comes from the fact that these machines tend to gather mildew, making them smell like a swamp.)

Energy and Temperature

In the previous post I detailed the First Law of thermodynamics, which says that if something happens to a system or object, the thing called the internal energy of the object undergoes a change

Don't pay attention to the actual equation. Just realize that the internal energy is

• increased by adding heat,
• decreased if the system does work, and
• increased if particles are added

And if the internal energy per particle (the average energy) increases, so does the temperature.

Modern folk have a big advantage over people 150 years ago when thinking about thermodynamics, in that we know that all matter on Earth is made up of atoms. The internal energy is therefore understandable from an elementary point of view: the atoms are whizzing around (in a gas), jiggling vigorously (in a liquid), or jiggling a bit (in a solid).

Now I want to talk about what temperature is. An object or system is made up of a bunch of atoms. Let's discuss a cup of hot coffee as our example. It's a liquid, and so the particles are all moving around, and they knock into each other a lot. Each particle has some speed, and hence a kinetic energy . All of their energies are different, but we don't really care what a given atom's energy is; we only care about what the average is. (Later we might be interested in more details.)

Think of the atoms in the liquid as people in the United States, and the amount of kinetic energy the atoms have as the amount of money the people have. Then, the temperature is determined by how rich the average citizen is. In physical terms, take the total energy of all the atoms and divide it by the number of particles---the higher that average is, the higher the temperature.

Let's see, from some examples, whether or not this analogy holds.

Suppose that one day Canada was annexed by the US. Since Canada is roughly as wealthy as we are, the average wealth would be about the same in the newly expanded US as it was before it added the new territory. The total amount of money increased, but the number of people increased proportionally.

Similarly, if you combine two cups of coffee, both at the same temperature, the resulting mixture has the same temperature as the two cups had before. The total internal energy went up, but the number of particles went up proportionally, so the average energy stayed the same. Thus, there is no change in temperature. This is, of course, what we expect if we add liquid at the same temperature.

Now, instead, suppose the US annexed Mexico. The total wealth would increase, but the number of people coming in is greater per dollar. You've added one group with a high average wealth to another with a (much) lower wealth. As a consequence, the average wealth decreases.

So, if we add cool cream to our coffee, what happens? Of course, the mixture is cooler! But by that, we specifically mean that the temperature decreased. We added a substance with relatively low average energy to one with high average energy, which drags the overall average, and hence temperature, down.

But your coffee can also cool down when it's just sitting on your desk. How does that work?

When we sit down for a cup of coffee (usually very hot in order to brew properly) we have to wait for it to cool. You might quickly realize that there is steam coming off of it, or you might notice that the air above the coffee is much warmer than room temperature and it's "clammy", which is to say that if you hold your hand over it for awhile and take it away your hand will be damp. What you feel is not only hot air, but actual water molecules in vapor form. But why exactly does this cool the liquid down?

What is happening is that some of the atoms in the coffee have a higher energy than other ones. The atoms in the coffee with the highest energy jump out of the water, forming a hot layer of air and water vapor just above the cup. Just removing atoms doesn't of itself reduce the temperature. However, since the fastest atoms are the ones that jump out, the internal energy per particle (which is to say, the  average energy of the particles) decreases, and this does reduce the temperature. If you want to speed the cooling up, you should remove the layer of hot air/vapor above the cup as soon as it develops. If you do this, then you make it possible for the next-fastest molecules to escape, reducing the temperature yet more. Removing the lid helps a lot, as it gives a lot more molecules the change to drift away from the cup, making room for new water molecules to take their place. Blowing over the top of the cup helps too, as you quickly get the hot atoms out of the way. So this is how coffee cools. Of course, you knew that! Blowing on stuff cools it. But the reason that it works is that the fast atoms jump out, you clear them away immediately by blowing, and then the next fastest jump out, etc. Each time you do this, the temperature drops because the average energy drops.

When you are cold, one of the things you do instinctively is rub your hands together, or rub your arms with your hands. This warms them up by way of friction. That is, we have heated something up by motion. Caveman knew how to warm up his hands this way. He knew that rubbing made things warmer. He knew that if he struck a flint or rapidly turned a stick against tinder he could make fire. In short, caveman knew a simple form of the First Law of Thermodynamics:

In light of this, then, you may wonder why scientists until the mid-19th century believed that heat was a thing, little "particles of warmth" called caloric. They thought when you burned wood you were releasing its caloric, and the pot of water you were boiling was absorbing the caloric. The more caloric you had, the higher the temperature would go. The theory, though wrong, had an internal consistency when it came to analyzing the operation of steam engines, the popular topic of the day. And it was certainly appealing: we can all get our heads around little particles flowing from one place to another.

At the same time, people were developing the idea of energy. Energy, to them, was nothing other than the ability to push things around and get them moving. Two kinds of energy were recognized: kinetic energy (the energy associated with a thing moving) and potential energy (stored energy against a force field like gravity). If you were moving, you could crash into something and make it move (do work on it), and if you had already done work lifting a weight against gravity, that work you had done would translate into the motion of the weight when you let it go. There was no real identification of other forms of energy, such as chemical, thermal, or electromagnetic, that we now talk about.

As we know, energy is something that is conserved. If you have some energy in a box, and you don't let any energy into it or let energy out of it, then the stuff in the box has some amount of energy in it (say, for instance, 50 joules), and that amount never changes. We also say that mass is conserved, so that if you have some oxygen molecules in a room, no matter what you do chemically, the oxygen atoms are always somewhere. Maybe they each joined with 2 hydrogens to make water, or were consumed while something burned to make carbon dioxide, or whatever; but if you look carefully, you will find the atoms somewhere: oxygen atoms are conserved.

Well, at the time, people had no real expectation that energy was conserved! The very first physics problem you can think of demonstrated no apparent properties of energy conservation. Suppose I hit a baseball into the air. Where did the energy that made the motion of that baseball come from? Well, it came from me, but where did I get it? I wasn't moving, I didn't have any identifiable potential energy. It seems that I created the energy out of nothing. Now the ball lifts into the air and momentarily stops at the apex of its trajectory. All the kinetic energy has been translated into potential energy. This was understood. But once the ball falls back to earth, it strikes the ground and stops. Where did the energy go? It seems that it was destroyed when the ball hit the ground. The box is the baseball stadium, and some energy inside it was created and then destroyed. Energy, it seemed, wasn't conserved.

When people thought about thermodynamics in the 19th century, they thought about steam engines. Trains, riverboats, these were objects of thermodynamics. And both had one thing in common: they involved the boiling of water. And everybody knows how you boil water. You burn something like coal, wood, or oil underneath a pot of water, and after awhile, the water heats up and boils. The more heat you added to the water, the more steam came off. Energy? That didn't seem to come into play.

In light of this, why not believe in something called caloric? Isn't it reasonable that the things you use to heat (oil, wood, coal) have caloric in them, and when you burn them the caloric goes into the water?

But one day a guy, Benjamin Thompson, was engaged by the British government to make cannons for its army. Because cannons needed to be very smooth on the inside, you couldn't just cast them in iron. You cast the general shape, and then used a very big drill to bore out the firing chamber. That way cannonballs would run down the muzzle in a smooth way and not blow the cannon apart.

Anybody who's ever worked with metal knows that you have to keep it cool while cutting it, so Thompson kept water in the cavity as he drilled it out. While boring out the cannon, he put a thermometer inside it, curious as to what happened to the liquid during the process. The story goes that to his surprise, the water's temperature was increasing. After 2 1/2 hours of drilling, the water actually came to a boil.

Though Thompson soon lost interest in the problem, James Prescott Joule knew that there was something to it, and endeavored to be more precise. What he thought was that if energy was put into a system in some way, and that energy was no longer visible at a later time, that the energy must show up as heat. This is simple to prove: He devised the machine depicted in this video:

Two weights were lifted into the air by the operator, giving the system a potential energy . When these weights dropped, they turned a paddle inside a container of water. In each cycle, Joule observe that the temperature increased by the same amount! This was indisputable proof of the following statement of the First Law:

If a system appears to lose energy, in reality the energy went into heating the object.

This changes everything. Going back to the previous example of hitting a baseball, the energy "created" is actually converted from the chemicals in the player's body by being burned. The energy "destroyed" actually shows up as a rise in the temperature of the baseball and the earth where the ball struck the ground. The whole system had some amount of energy, and it was the same throughout. Energy is conserved.

It was also realized that temperature, which everyone has some notion of, corresponds somehow to how much energy is inside a thing. We could call it the internal energy of the object. Take for instance the baseball. It has a certain temperature, which is about room temperature. What this implies is that it has an internal energy that corresponds to the temperature. If you tell me the temperature, I can tell you how much energy is stuffed into it. This has nothing to do with it moving (which would be kinetic energy ) or potential energy () which are about the motion of the whole object. This was energy the object had stuffed inside it when it's just sitting on the ground doing nothing---the vibrations of particles that it's made of.

From this point of view, denial of atomic theory (that all matter is made up of atoms) began to seem preposterous. For surely somehow this internal energy was in fact the kinetic and potential energy of the little bits inside the object.

With heat, work, and internal energy, we can enunciate the first law in a semi-technical form:

If no particles leave}, then , where is the change in internal energy, is the heat added, and is the work done by the system.