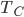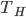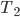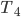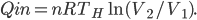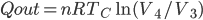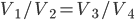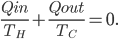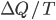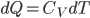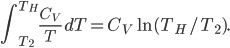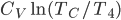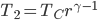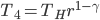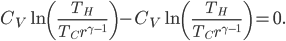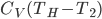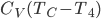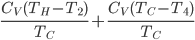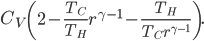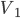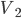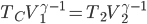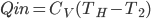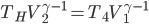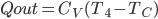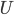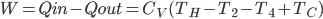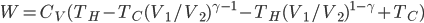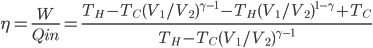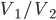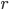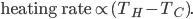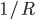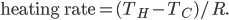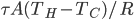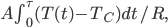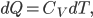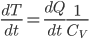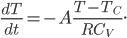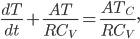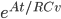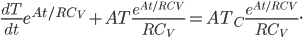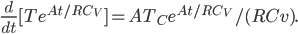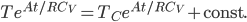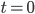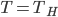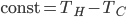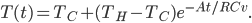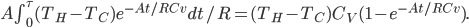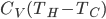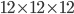So far I've kind of just talked about heat  moving from one system to another, without much regard to how that transfer actually happens. The way that heat actually gets around is hugely important, so we can't keep avoiding the issue.
moving from one system to another, without much regard to how that transfer actually happens. The way that heat actually gets around is hugely important, so we can't keep avoiding the issue.
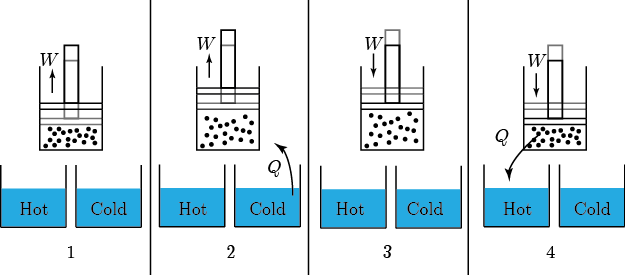
Of course, we know that heating is the transfer of energy from one set of atoms, which I'll call object 1, to another, object 2. Aside from exchanging particles, what are our options for how to effect this? There are 3:
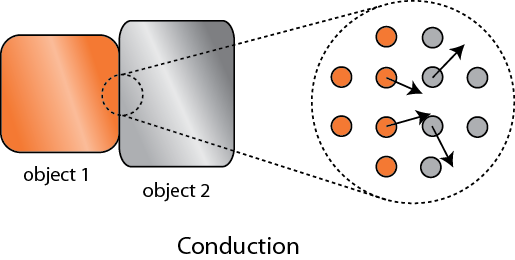
Firstly, we could put the two in physical contact, so that the atoms of 1 can hit the atoms in 2. For a solid this is easy. For a liquid or gas to do this we have to put some kind of membrane between the two objects to keep the particles from mixing. No big deal. This is called conduction. When you put your steak right on the grill, the heat is conducted from the hot grill into your steak because the jiggling iron atoms in the grill knock into the atoms in the steak and start them moving faster. This relies on there being a significant amount of area in contact.
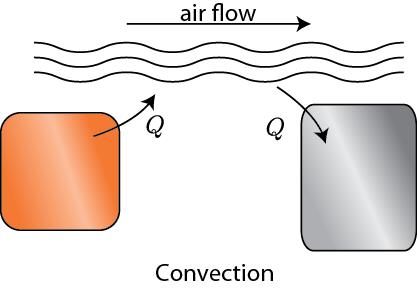
 Secondly, we could use some medium, like air, to transfer the heat. That is, we could let object 1 heat some air, and then blow that hot air over object 2. The net effect is that heat was transferred from 1 to 2. This is called convection.
Secondly, we could use some medium, like air, to transfer the heat. That is, we could let object 1 heat some air, and then blow that hot air over object 2. The net effect is that heat was transferred from 1 to 2. This is called convection.
 Thirdly, we could use the fact that all objects emit electromagnetic radiation to transfer the heat. Object 1 radiates light, and the light carries energy. When that light hits object 2, it can absorb it. This is called radiation.
Thirdly, we could use the fact that all objects emit electromagnetic radiation to transfer the heat. Object 1 radiates light, and the light carries energy. When that light hits object 2, it can absorb it. This is called radiation.
 That's basically it. Conduction, convection, and radiation are the ways to get thermal energy from one thing onto another. I suppose you add in "an engine", but the engine itself is really some combination of these 3, so it's superfluous.
That's basically it. Conduction, convection, and radiation are the ways to get thermal energy from one thing onto another. I suppose you add in "an engine", but the engine itself is really some combination of these 3, so it's superfluous.
There are actually grills and ovens that do each of these things. Grills and pans use conduction, by putting the food in contact with them. This heats the side in contact very quickly. Since the food doesn't do a good job conducting the heat through itself, this mainly cooks the meat near the surface, allowing for searing. Convection ovens offer more even heating while still being relatively fast because they heat all sides of the meat which are accessible by the air flow. A normal oven uses radiation and heats the air inside it so that heat goes into the food from all sides. Is that conduction or convection? I have no opinion. Recently, some grills offer infrared heating, which uses radiation that isn't visible to cook.
What accounts for the rate of heating? If you put two things at very different temperatures together, heat flows quickly from the hot one to the cold one. If the two objects are not too different, the the heating is slower. The heating rate is usually proportional to the difference in temperature
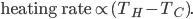
This isn't very surprising. Now, if we want an equality we just need a constant out front. In this case we call the constant 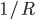 .
.  doesn't have a name, so people just call it
doesn't have a name, so people just call it  , or R-value. Then
, or R-value. Then
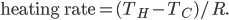
Large R-value is a very good thing if you're trying to insulate something like your house. Then, even if it's very cold outside and very warm inside, the heating rate won't be too big, making you have to run your furnace all the time.
In the US, the R-value given for insulation is in ft2 F h/BTU. Supposing that it's 75°F inside and 30°F outside, if you have R-13 insulation, the house will lose 3.5 BTU per square foot of wall every hour. To maintain the temperature, the furnace has to therefore put this much heat into your house every hour. Windows have a much lower R-value, with a regular air-filled window having a value of 2, so the heat needed for every square foot of window is higher by a factor of about 6.
Now here's a relevant question we can answer: when you leave the house on a cold day, should you leave the heat turned on, or turn it off until you get back? After all, when you get home the house will be really cold, so the heater will have to run for a long time to restore the temperature. If you leave it on, it only has to run a little bit from time to time. On the other hand, what if you left for 2 months? Surely you wouldn't argue that the heat should be left on.
The answer is that you should turn off the heat. Because the heating rate (or loss of heat by the house) is bigger when the temperature difference is bigger, you're always better off letting the temperature fall.
Important!
Suppose you leave for a time
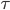
. The total amount of heat you need to add if you leave the heater on is
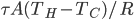
where
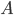
is the area of wall you have. But if you turn it off, the heat needed to reheat the home is
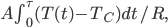
because the temperature changes with time. We have to solve for
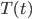
. Note that by the definition of heat capacity,
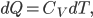
so
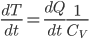
where
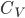
is the heat capacity. We have to be mindful here. The derivative is decreasing so we must use the negative of the heating rate
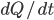
given above:
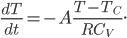
We can rearrange a bit,
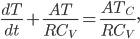
and multiply through by
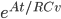
to obtain
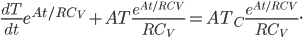
The left-hand sum is the derivative of a product,
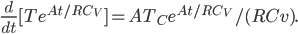
Now integrate both sides with respect to time:
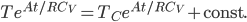
The constant is determined by the initial value, which is that at
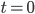
,
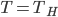
. So
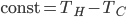
, and
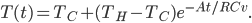
The heat needed to be supplied to restore to
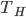
if you turned it off is therefore
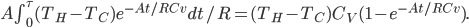
As
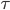
gets large, this reduces, as of course it must, to
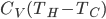
. But the expression above is always less than
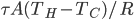
.
The heat capacity of a
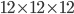
foot room is about 2500 BTU per Fahrenheit. So, we could plug everything in and see, on a day where the outside temperature was 32°F and the inside was 75°F, how much heat was needed to maintain that room with an estimated R-value of 5, with all the doors, windows, and walls taken into account.
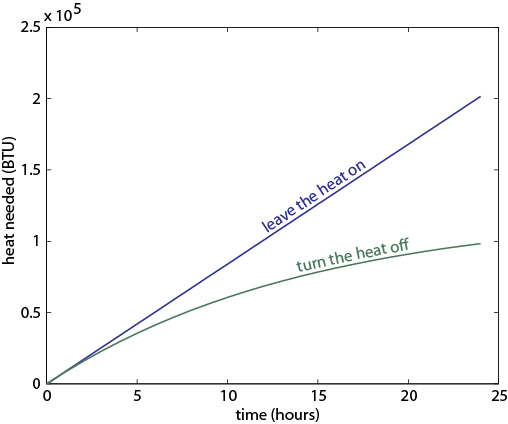
The blue curve is what happens if you leave the heat on and the green curve is if you turn it off. After a few hours, the amount of energy you waste is much lower if the heater is turned off.