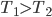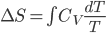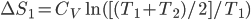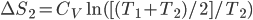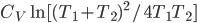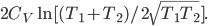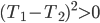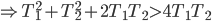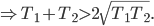It's hard to say much of anything about  particles if you don't know anything about the system they're in. When air is flowing through a tube, for instance, it's a constantly changing, turbulent mess. However, we can say a lot about systems that have reached equilibrium. Equilibrium is what happens when you leave the system sitting for awhile without doing anything to it.
particles if you don't know anything about the system they're in. When air is flowing through a tube, for instance, it's a constantly changing, turbulent mess. However, we can say a lot about systems that have reached equilibrium. Equilibrium is what happens when you leave the system sitting for awhile without doing anything to it.
Some kinds of equilibrium are obvious. If two systems are in direct thermal contact, so that they can exchange energy (by heating), then equilibrium is when the temperature is the same. If two gases are in two chambers separated by a movable wall, equilibrium is when the pressure is the same. And if the system is both in thermal contact and separated by a movable wall, both of these must hold.
So far we've talked about relatively straightforward quantities. Internal energy, volume, temperature, and pressure are simple to define. But because of the 2nd law, we have another quantity that defines equilibrium: entropy. This quantity will be as big as possible when the system has settled down, so it's unlike what we've seen before.
First, we should check with a simple example. If we have a cup of water at 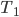 and another cup at
and another cup at 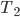 , then we know that if we mix them they will exchange heat until the temperature has equalized. This is clearly irreversible. Let's think about how the entropy changes, which, as I've said, is heat added divided by temperature it was added at.
, then we know that if we mix them they will exchange heat until the temperature has equalized. This is clearly irreversible. Let's think about how the entropy changes, which, as I've said, is heat added divided by temperature it was added at.
Of course, the final temperature of both will be halfway in between the two temperatures, the average, 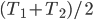 . As for the entropy, it will decrease for the hotter water and increase for the colder water. The heat that leaves one is the same as the heat that goes into the other one. But, the entropy is the heat divided by temperature, and since the temperature for the cold one is lower, the heat divided by temperature will mean the cold one will gain more entropy than the hot one will lose. Thus, for the universe, the change in entropy is positive. Calculating exactly is a little complicated, since the temperature is changing the whole time.
. As for the entropy, it will decrease for the hotter water and increase for the colder water. The heat that leaves one is the same as the heat that goes into the other one. But, the entropy is the heat divided by temperature, and since the temperature for the cold one is lower, the heat divided by temperature will mean the cold one will gain more entropy than the hot one will lose. Thus, for the universe, the change in entropy is positive. Calculating exactly is a little complicated, since the temperature is changing the whole time.
To get to equilibrium, the system makes the temperatures of the water the same, and it also raises its entropy by as much as possible. Once the temperatures are equal, there is no way for the system to raise its entropy anymore, so it stops. If things are left alone, the condition that they come to is naturally one that maximizes entropy.
So how often do you increase the entropy of the universe? All the time! Putting ice into water, heating water to brew coffee, driving your car, standing in the Sun, burning calories to keep your heart running: you and everything around you are entropy generating machines, because you all are constantly doing things that are irreversible.
Now, anybody who's seen a TV spy show knows that everything in the universe radiates "heat", which in the usual cases is dominated by infra-red light that IR cameras can see. Any object at non-zero temperature (that's everything) is radiating. That means that in the end, all objects in the universe will heat everything else. But that's irreversible. So eventually everything will become one temperature, energy will spread out as much as possible, and nothing else can happen. It's the end of the universe!
This is called the "heat death of the universe", and there really aren't too many convincing arguments against it. Entropy gets maximized, and nothing else happens ever again. There are a few reasons to think this may not happen, and we still have a lot of uncertainty about what exactly our weird universe is doing. But in the end, what happens to this universe may not be so different from what happens when you mix two cups of water at different temperatures.