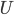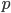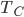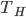Now that we know the 2nd law, let's look at some consequences. To review, the 2nd law says that there is no way to turn heat completely into work without changing something else.
If we had a piston, and we heated it and let the gas inside it expand, it would do work pushing against the atmosphere. If we do it slowly, the temperature in the piston stays the same, and so its internal energy is unchanged. Then, the first law says that 
. That violates the 2nd law! We took heat and turned it all into work! No, we didn't: the law says that we can't turn heat into work without changing anything else, and something has changed---namely, that the piston is pushed out, when it used to be in.
Machines, though, have to cycle. They have to be in the same state at the end of an operation as when they began, so that they can keep being used. The cylinders in your car engine wouldn't be much good if, at the end of the combustion process, they weren't put back in a condition to combust again. It's the process of getting the piston reset that ends up making us have to waste.
An engine can be efficient or inefficient. The human body is relatively inefficient in converting heat through burning calories into work moving your body around. But what about a car engine? How should we determine what makes an engine efficient?
Let's define efficiency this way, which is pretty natural. You take the amount of work the machine does in one cycle and divide it by the heat you had to put in to get that much work. The First Law implies that the efficiency could be between 0% and 100%, with 0% being totally inefficient (taking in some heat but wasting it all and doing no work) and 100% being perfectly efficient (taking in heat and doing just as much work). But the Second Law says it is actually going to be less than 100%, since you have to waste some heat.
Try to guess what the efficiency of a highly evolved, modern day, computer aided internal combustion engine is. The number is actually about 18%. For every Joule of heat you put in by burning gas, you get a lousy 0.18 Joules of work out. One question that we'd like to know is, what is the best possible efficiency? What percentage could we theoretically achieve if we were smart enough to work it out?
I will now describe to you the most efficient engine possible, and yes, you can build an engine that is just as efficient. (You cannot, however, build this exact engine, nor would you want to.) For this hypothetical engine, we only need some gas inside a piston and two reservoirs of heat at different temperatures. We'll say the piston has no friction. The cold bath could be some lukewarm water, and the hot bath some water that we boiled---it doesn't matter. It just needs two reservoirs of heat at different temperatures. For the sake of argument, we'll say the hot reservoir is 100°C and the cold reservoir is at 23°C.
This engine has four strokes:
- We start out with the gas inside the piston at 100°C and at a higher pressure than the outside air. We run a stream of the hot water over the piston. The pressure of the gas is higher than the outside air, so the piston will push out. The gas inside pushes out the piston but stays at the same temperature. So, its internal energy is the same before and after, which means heat absorbed is equal to work done:
. It absorbs exactly as much heat as it needs to maintain 100°C while doing the work. (This is called isothermal expansion, because the temperature stays the same.) - The stream of water is turned off while the pressure inside the piston is still greater than the outside pressure, so it continues to expand. During this, no heat is absorbed or expelled, since no water is flowing. Then, the internal energy must decrease by
, the work it does in pushing the air outside the piston. Once it gets to room temperature, we proceed to the next step. - The stream of room temp (23°C) water is now turned on, and cool water flows over the piston. And now we have to give the piston a push. Yes, we have to give back some of the work done. But since we keep the water flowing, all it does is make the system give up heat; it stays at the same temp. The heat the water absorbs is
. - Finally, we remove the room temp water stream and push the piston back to the starting point, whereupon we can perform another cycle. The temperature increases back to 100°C. The internal energy changes by
.
Ok. Now it's a matter of accounting. How much heat did we absorb? 
. How much work did we do? 
. We did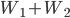 
of useful work but had to give back 
of it to reset the engine. We also had to throw out heat 
as waste. The efficiency can now be calculated easily for an ideal gas.
Important!
The work done in the first stroke is done isothermally. The first law for
then says that work is equal to heat, so
In the second stroke there is no heat, so the change in
is the work done, 
. When no heat is added, then the expansion is called adiabatic, and there is a simple law for that:
That is,
is the same at the start as it is at the end of the process.We can write this in terms of
instead of 
by using the ideal gas law
So since the temperature at the end is
, we have
In the third stroke, it's isothermal again:
And in the final stroke, which is again adiabatic,
. However, since it went back to 
, the internal energy must have changed the same as in stroke 2, which means that 
. As before, adiabatic compression tells us that 
. The efficiency, 
, is defined as the total work done divided by the heat absorbed from the heat bath.
; it was a wash.)We can work out the numerator pretty easily:
But according to the above,
So,
Since
, then,
This engine, called the Carnot engine, has an efficiency that is equal to the hot temp, minus the cold temp, divided by the hot temp. If the cold bath is at room temperature and the hot bath is a piping hot 1000K fire, the efficiency would be 70%. To increase the efficiency, we would have to use a colder cold bath.
But notice that this is far less than 100%. 70% is a hell of a lot better than 18%, and so seemingly we'd do well to work on getting an engine with this efficiency. (Actually, there is such an engine, called the Stirling engine, but they aren't used in many technological applications.)
But what is the big picture here? A hot gas shoved something, which we can use for transportation, lifting, or what have you. The rest was trying to get the system back to its original state. In doing so we had to dump out some heat, and we had to put some of work back in. However, we pushed the gas while it was cooler, and thus it didn't take as much work as the gas did during the initial stage. If you have to push back on the gas, it's best to soften the gas up a bit by reducing its temperature.
But the real big picture is that it is a law of nature that no engine is perfectly efficient. Suppose that you have thought of a brilliant way to keep a machine going forever. You'll take the work the engine does and convert it to heat. Then you'll use that heat to keep driving the engine. But the 2nd Law says that can't happen. Some of the heat you've taken in is not converted to work, and therefore the original heat cannot be turned into an equal amount of heat used to keep driving the engine. You cannot make an engine that goes forever, a perpetual motion machine, because in every cycle you have to waste heat. This is true even for a hypothetical frictionless engine.
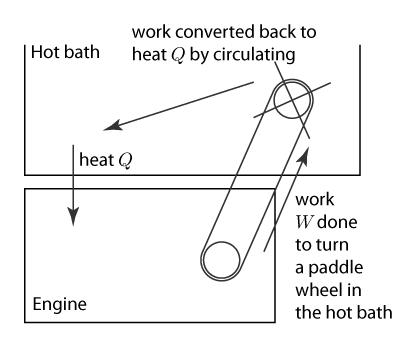
A fictitious perpetual motion machine. The scheme is unworkable because the work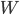 
is actually less than 
.