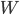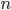Thermo for Normals is a short book (~100 pages) I wrote that conveys the basics of thermodynamics without all of the mathematical complexity. Over the next year I will be posting 1 or 2 sections of the text per week. I don't know whether I will ever try to publish it in any other form, though perhaps as an Amazon e-book it wouldn't be a bad idea. Questions, comments, criticisms, and corrections are welcome.
The conserving universe
Last time we discussed the laws of Isaac Newton, which are true (except for extremely tiny things). However, we almost never use them. The reason for this is that they are intuitively easy to understand for simple things, but hard as hell to understand for real things. So, instead, it's better to talk about energy and momentum, each of which is conserved in a system. That way, problems come down to simple accounting.
The first conservation law is the conservation of energy. It states that
What the heck is a closed system? Draw an imaginary box around something. As long as nothing outside the box does anything to something inside the box, then the stuff in the box is a closed system. Energy is roughly conserved on a pool table, so if you draw a box around the pool table, no energy goes in or out of that box, except for when the cue stick is involved, since that comes from outside the box.
But what the heck is energy? I can't tell you. It's like money. What is money? I can't say. But I can say what money does. You can trade money for goods and services. People who produce a lot (or steal a lot, or who inherit a lot, or who do banking ...) have a lot of it. Here's what energy does: if an object has energy, then it can do work, which means it can give its energy to other things. If it's going fast, it has a lot of energy, and can do a lot of work. We normally talk about an amount of energy in Joules. If you have something creating a Watt of power, it's creating energy of 1 Joule every second.
We only recognize 4 kinds of energy. The first is the energy associated with motion. If a particle is moving, it has kinetic energy. This is equal to 
, where 
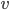is its speed and 
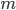its mass.
Important!
Since work is
, and work done equals change in energy, we can find the energy of a free particle by doing work 
on it and finding its speed.Kinetic energy is equal to
Kinetic energy is like cash on hand. You can see the particle has it, and it can spend it immediately by exerting a force on something for awhile, which transfers energy to it.
The second kind of energy is energy stored against a force, called potential energy. Potential energy is like energy the particle is owed. At any time, a mass's potential energy can be converted to (traded in for) kinetic energy (motion), and vice versa. If you lift a weight a distance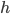 
above the ground and set it on a table, you've given it energy 
, but it hasn't shown up as motion. It's saved up in the bank. But when the weight falls, it cashes in the energy and starts to move. Some examples of forces that store potential energy are gravity, electromagnetic forces, springs, and elastic forces.
An object can also have negative potential energy, which would mean that the particle owes energy. To get it free you have to give it some energy. We all have negative potential energy because of the Earth: to get free of the Earth someone has to give us a lot of energy (I owe about 4 billion Joules). Note that forces like drag or friction do not have potential energy associated with them.
Thirdly, you can have energy stored in electromagnetic fields in the form of light. This energy too can be converted into other forms of energy. The reason why the Sun or a hot lamp makes you hot is that energy is being delivered to you via the light. Induction stove tops send energy across a gap from the range to the pot via very low frequency (non-visible) light.
Finally, there is mass energy, or energy associated with just existing. The equivalent energy of some mass is given by 
, when something is standing still. If somehow you create a reaction where the mass changes (it can happen!), then some amount of energy was released. We shall not have occasion to talk about this going forward, since it only happens in nuclear reactions, but it should be listed for completeness.
Now, if the system is not closed, then energy can be put into the system by work done from the outside. Energy can also go out of the system if work is done by the system on the outside world. Work is nothing more than pushing over a distance. If you push something with force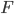 
and it moves a distance 
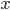in the direction you push, the work you did on it was 
. This is why energy is measured in units of force times distance. As I said before, it's usually measured in Joules. Other popular units are ergs, calories and BTUs.
Important!
It is possible to prove energy conservation directly from Newton's 2nd law. Start with
and multiply by
on both sides, moving everything to the left-hand side:
Let
or 
. Then, this is
The term in parentheses is constant in time because its derivative is zero. And the stuff in the parentheses is the energy. Therefore, energy is conserved in a system.
The next law is that of conservation of momentum, which holds in any system unless there's an outside force.
Now, if a particle hits a wall, everyone knows that it rebounds, so that its velocity perpendicular to the wall switches direction, meaning momentum is not conserved. The wall, however, is an outside force, so this is fine. Momentum is only conserved among internal collisions. Collisions with the outside means momentum will change.
Important!
This follows directly from the 3rd law. Suppose we have
particles in a box that interact with forces 
on each other. Then,
The final sum is guaranteed to be zero by Newton's 3rd law.
Now, note something interesting here. Suppose I make my "closed" system, which I'm drawing my box around, be the entire universe. These two laws say that energy and momentum are conserved. That means that the amount of energy in the universe is always the same. However much it started with, it still has that much. Momentum is the same. If you added up all the masses moving to the right times their speeds, you would find it was identical to all the masses moving to the left times their speeds.
That's it for mechanics. We have it out of the way, and can start talking about thermodynamics.