Sudoku puzzles are classified according to their difficulty. My old newspaper, the LA Times, did so as Gentle, Moderate, Tough, and Diabolical. Sites like Daily Sudoku have basically the same division, though the names are different (hard and very hard instead of tough and diabolical). Difficulty is determined by the techniques needed to solve the Sudoku. Simple elimination techniques, naked twins, and indirect inferences come up in Gentle and Moderate. Tough and Diabolical additionally require more advanced stuff.
Hidden twins is an advanced technique I've already talked about, where candidates are eliminated based on a twin that isn't readily apparent. This is a bit tricky, since you're actually adding a candidate to a triplet that isn't there so that it matches two other squares. With practice, though, hidden twins are easy to spot.
However, we need to go beyond those techniques to solve a very hard puzzle like the following that I got from Daily Sudoku:
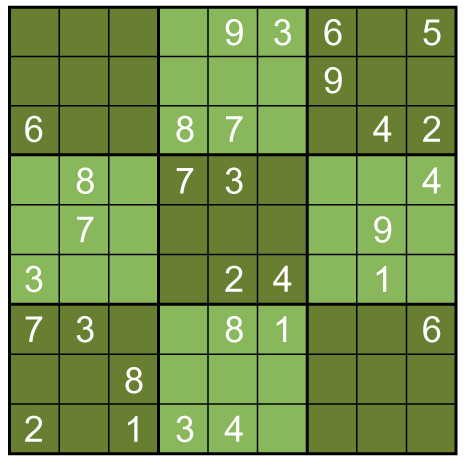
Using a combination of box, row, and column searches, twins, and indirect inferences, we can get to this point with the puzzle (I've put in all pencil marks):

To see how I got this, see the end of this post. You can convince yourself that the puzzle cannot be solved further using any basic techniques.
The first thing I notice is that the first row has hidden twin in 1 2. See how squares two and four of that row are the only squares with those numbers? Thus, we can remove the candidate 4 from Box 2 square 1.

This lets us solve for the 4 in Box 2, and eliminate a few other candidates. Here is the puzzle as it stands:

Not much progress. However, I think of a Sudoku like this as a delicately balanced thing. If the puzzle wasn't just so, it would collapse. Solving for even one more square could lead to many solutions. Finding that is the key to finishing tough puzzles like this.
What I'm looking at is squares that contain a cycle of three digits that can "see" each other. So, for instance, the 3 7 in Box 1 can see the 1 7 in Box 3. The common digit is 7. So the question is, can either of these squares see the other pair, 1 3? It just so happens that the 1 7 can see the 1 3:
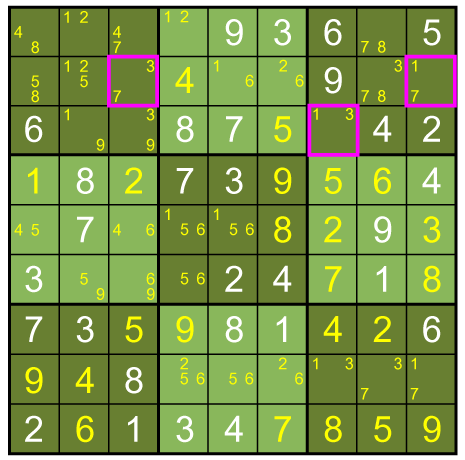
How does this help us? If the leftmost highlighted square were 7 then the lower square must be 3. If the leftmost square is 3, then the lower square is also 3. Thus, the lower highlighted square is 3.
We actually got a little bit lucky. Under other circumstances, this would only have allowed us to eliminate 3 as a possible in Box 3 square 5. That itself would have led to a number of solves, though. Like I said, it's a fragile structure.
Because the structure of the highlighted box vaguely resembles a Y, this tends to be called a Y-wing elimination. I think it's kind of a silly term, and rather like to think of it as a cycle rule. In this case it was 3 7 sees 1 7 sees 1 3. The cycle is complete. You start with a square with two possibles, and look around for any square with a pair that has one number in common. If you find one, see if that square sees any squares with the complementary pair. If so, you have found a Y-wing. Then just use basic logic to determine what candidates can be removed.
With just this one technique, the puzzle is solved very quickly. The finished puzzle is below, along with the solution to get to the second step.
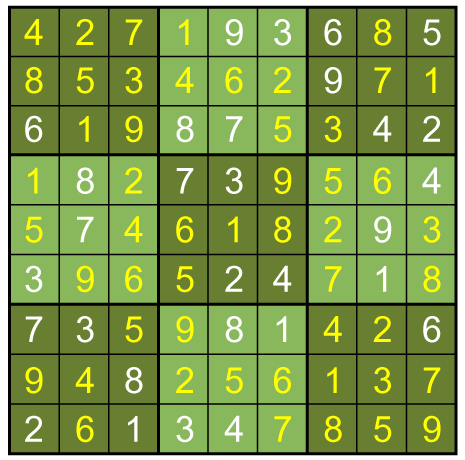
Solution to get to step one: The labeling scheme is box,square, where numbering runs from left to right.
5,6 = 8
4,1 = 1 (indirect from box 5)
6,2 = 6
7,4 = 9 (column)
9,9 = 9
8,1 = 9
5,3 = 9
6,6 = 3
2,9 = 5 (enumeration)
9,1 = 4
9,2 = 2
7,3 = 5
7,8 = 6
4,3 = 2
6,1 = 5
6,4 = 2
8,9 = 7
9,7 = 8
9,8 = 5
6,7 = 7
6,9 = 8





