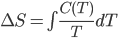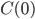Here I've been blabbering on and on about entropy, but all I've really talked about is changes in entropy. Irreversible things miss opportunities to do work, and that makes entropy go up. But what is the entropy of, for instance, a bottle of gas? It has pressure, temperature, volume, and internal energy. If the gas is being used in an engine, all of those quantities get reset by the end of the cycle. And entropy change for the engine is also zero, which indicates that there's an absolute entropy 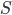 . For a certain jar of gas maybe it's 100 J/K---whatever, there should be a number!
. For a certain jar of gas maybe it's 100 J/K---whatever, there should be a number!
It really ought to be simple enough. If we find the conditions under which 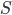 is zero, then we can just add heat and calculate what
is zero, then we can just add heat and calculate what 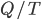 is.
is.
The thing is, it's fairly easy to say what it means that 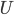 ,
, 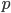 ,
, 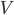 , or
, or  is zero.
is zero. 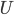 is the internal energy, so if all the atoms are standing still,
is the internal energy, so if all the atoms are standing still,  . Since
. Since  is in some way a measure of
is in some way a measure of 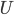 , it is also zero when the atoms aren't moving. If the atoms aren't pushing on anything, their pressure is zero. And if the atoms are in an extremely small space, the volume is zero.
, it is also zero when the atoms aren't moving. If the atoms aren't pushing on anything, their pressure is zero. And if the atoms are in an extremely small space, the volume is zero.
But what should the entropy be when 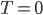 ? I suppose we could say it's 32 J/K, but let's be sensible and say that entropy should be zero when
? I suppose we could say it's 32 J/K, but let's be sensible and say that entropy should be zero when 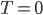 .
.
Seems simple enough. After all, where else would it be zero? You certainly can't take heat out of something where none of the atoms are moving. Ok, so if 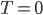 K, the entropy is zero.
K, the entropy is zero.
Before we start talking about what the consequences of the 3rd law are, I need to clear something up about heat capacity. I said that the heat capacity is the amount of heat you have to add to raise the temperature by one degree. And then I stated some numbers for a few substances. I said that for liquid water the heat capacity was 1 cal per cm per K. But that's only partly true. It's 1 calorie at 289 K, but there's no reason to think it's the same for all temperatures. And in fact, it's not.
per K. But that's only partly true. It's 1 calorie at 289 K, but there's no reason to think it's the same for all temperatures. And in fact, it's not.
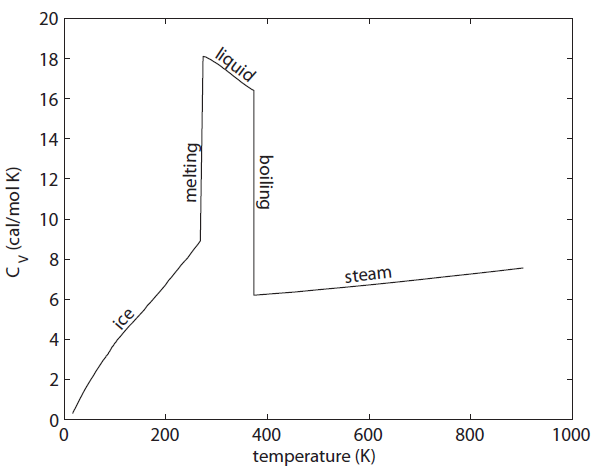
The heat capacity of water per mole across the temperature ranges from 0 K to 900 K. Low temperature measurements made by W.F. Giauque and J.W. Stout, Jour. Amer. Chem. Soc. 58, 7 (1936). Liquid and steam values readily found
The graph above shows the heat capacity of 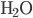 measured by experiments (at constant volume). The units here are calories per mole per Kelvin instead of per cubic centimeter. There are several interesting things about this. First is that the liquid phase can hold a lot more heat per mole than either ice or steam can. This is what we thought might happen when we discussed this earlier. But also look what is happening as we lower the temperature of ice toward 0. The heat capacity is going to zero! And pretty rapidly too.
measured by experiments (at constant volume). The units here are calories per mole per Kelvin instead of per cubic centimeter. There are several interesting things about this. First is that the liquid phase can hold a lot more heat per mole than either ice or steam can. This is what we thought might happen when we discussed this earlier. But also look what is happening as we lower the temperature of ice toward 0. The heat capacity is going to zero! And pretty rapidly too.
The heat capacity going to zero in ice is not a fluke; heat capacity goes to zero no matter what the substance is.
So, no matter what substance it is, near absolute zero the heat capacity is very small, and you can get a huge change in temperature from adding a small amount of heat.
Now, suppose we are trying to cool something down to absolute zero. We do this, of course, by way of a refrigerator, which takes in work and moves heat from the cold object (what we're trying to cool down) to another heat bath at higher temperature. The efficiency with which it does this depends on the actual refrigerator you use, but let's use the best possible one: a Carnot engine in reverse. The Carnot engine run in reverse between two temperatures takes in work 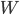 and moves removes heat
and moves removes heat 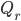 from the cold bath. The amount of heat can be shown to be the efficiency of the refrigerator times the work:
from the cold bath. The amount of heat can be shown to be the efficiency of the refrigerator times the work:
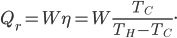
On the other hand, removing that much heat reduces the temperature of the cold bath by the heat capacity times the change in
 .
.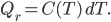
So the amount we reduce the cold bath temperature by is
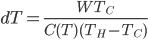
This is a conundrum. What it says is that if I put work
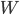 into my refrigerator every cycle, I get a small change in the temperature of the cold bath, but it's proportional to
into my refrigerator every cycle, I get a small change in the temperature of the cold bath, but it's proportional to 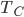 divided by
divided by 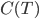 , the heat capacity. But both of these are going to zero! So it's a competition: if
, the heat capacity. But both of these are going to zero! So it's a competition: if 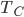 approaches 0 more rapidly than
approaches 0 more rapidly than 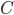 does, then it is impossible to reach absolute zero, because
does, then it is impossible to reach absolute zero, because 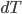 will just keep getting closer and closer to 0. On the other hand, if
will just keep getting closer and closer to 0. On the other hand, if 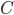 goes to zero faster, then it's very easy to reach absolute zero. I do not know of a simple argument for why the heat capacity goes more slowly, as it is a legitimately highly technical question (A decent treatment of the issues involved can be found in Ernest M. Loebl, Jour. Chem. Ed. 37,7 (1960)). Suffice it to say that
goes to zero faster, then it's very easy to reach absolute zero. I do not know of a simple argument for why the heat capacity goes more slowly, as it is a legitimately highly technical question (A decent treatment of the issues involved can be found in Ernest M. Loebl, Jour. Chem. Ed. 37,7 (1960)). Suffice it to say that 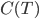 remains finite lower down that
remains finite lower down that  does, and so the amount we cool the object gets less and less every time. The consequence is that absolute zero can never be reached.
does, and so the amount we cool the object gets less and less every time. The consequence is that absolute zero can never be reached.
Not that people don't try. The lowest anyone has ever gotten was in 2008, when a lab in Helsinki cooled some rhodium metal down to 0.0000000001 K. People regularly get down to 0.001 K, and even 0.000001 K. But that's as good as you can do. Some people (including myself) think that the 3rd Law may as well just be this.
In any case you don't actually need to get to absolute zero to tell what the absolute entropy of something is. Just knowing that it should be zero at
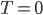 gives us a reference point so that we could actually state how much entropy a given system has. A gas of
gives us a reference point so that we could actually state how much entropy a given system has. A gas of 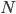 molecules confined in volume
molecules confined in volume 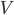 , with internal energy
, with internal energy 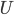 , has, for instance an entropy equal to
, has, for instance an entropy equal to
Ok, ok, I know this looks horrendous, but now you've seen it and you know that we can say with honesty that a given object has a certain amount of entropy, so that we don't just have to talk about changes.