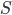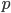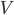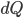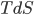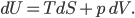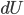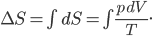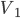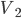I have to admit, I've been fibbing a bit. It is absolutely true that changing something's temperature by heating changes its entropy by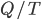 
. However, this is not the only way to change it. In fact, anything that's irreversible increases the entropy. And there are ways to decrease the entropy of a system without taking heat out of it (though there is no way to decrease the entropy of the entire universe).
Last time we talked about connecting a bottle full of gas to an empty bottle so that some of the gas would flow into the previously empty one, and that this was irreversible. As such there should be an increase in entropy from this; and indeed, there is. (Remember: something is irreversible if, watching a video of it going backwards, you see something that never happens.)
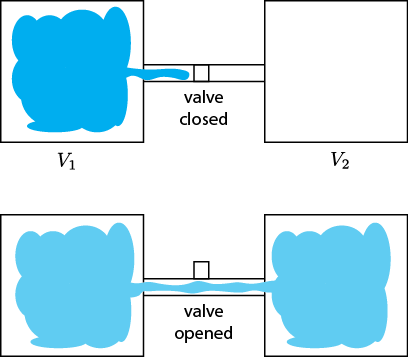
A chamber with gas is opened to a chamber that initially is evacuated, resulting in the free expansion of the gas into the new chamber.
Important!
A calculation of the entropy change for free expansion is not quite as straightforward as it was for heating. The fact is that even though the process is irreversible, surprisingly the entropy change is the same as for a reversible process. This is because 
is a property of a system independent of how the system got there, just like 
, 
, or 
. None of these variables has any history built into it.
Anyway, from the first law, we can replace 
with 
:
No work is done by or on the outside, so
must be zero. Then,
For an ideal gas, if the first bottle had volume
and the second bottle had volume 
,
So for 2 identical volumes, the gas expands but gains an entropy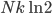 
. And the universe also gains that much, and you can never undo that, unless you want to wait a literally unimaginable time.
Now, as I said last time, you can force the gas to go back into the original bottle. To do that you have to do work, and to do work you have to use an engine (I use the term generally. A human can be considered an engine, anything that takes in heat and makes work is an engine). "Fine", you say, "I'll use a Carnot engine. The Carnot engine doesn't change the entropy of the outside at all, and by using the engine we press it back in and everything's just the same as it was.". Sorry, no. If you compress the gas, you do not put it back in the original state, because when you compress it you do work on it, which will heat it up. So it will be at a higher temperature, and to return it to where it was initially you have to reject some heat to the environment, which again means that the entropy of the universe is permanently higher than it was before you let the gas expand.
Entropy increase is permanent for the universe. It's a one-way street; once entropy is created, it simply cannot be undone.
Here's something to think about. If we pull out a piston with gas behind it, we have not done the same thing we just described. We did not let the gas freely expand, because we made sure that it did work as it expanded. The gas would cool, it's reversible. However, if we pull the piston out too fast, then it is like free expansion! So even in things that we think are reversible, we have to be careful to go slowly enough that the gas molecules can keep up; they have to sort of come to equilibrium before we keep moving on.
Another way to do something irreversible is to start a chemical reaction. Burning a hydrocarbon like methane (gas) in oxygen (gas) makes carbon dioxide (gas) and water (vapor), and releases a lot of heat. The reaction is irreversible. Now, modeling this system with a calculation would be hopeless, so I can't calculate from first principles how much the entropy will go up. But these can be looked up in tables, measured by people over the years. You can see a table of them, for instance, here. For each mole, methane (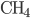
) has 186.3 J/K, oxygen (
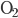) has 205.1 J/K, 
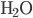(liquid) has 69.9 J/K, and carbon dioxide (
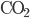) has 213.7 J/K. (All of these values are for room temperature.) The reaction is
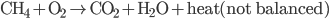
If you remember your chemistry, you know that this equation is not balanced, meaning that there are not as many oxygen atoms on the left side as the right side, not as many hydrogen atoms, etc. I.e., this is not the reaction that happens! Only once we balance it will we know how many moles of each actually go into a reaction. Ok, the right hand side has 3 oxygens, and the left hand has 2, so if we say that it makes two water molecules instead of 1, and 2 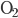go in,
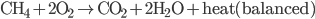
Now you can see that the equation has as many oxygens, hydrogens, nad carbons on the left as the right. The heat created is an amazing 800,000 J for one mole of 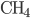. This heats the environment (at approximately 300K), creating an entropy of about 2500 J/K. So this is the actual reaction. Now if we look at the entropies (all numbers are in J/mol K)
or
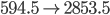
That's very interesting! Notice that without the 2500 J/K of entropy created by heat, the entropy would actually go down. But as you can see, with the heat included the entropy of the universe increases a lot in this reaction. And since burning is obviously irreversible, this matches what we would think. Doing something irreversible increases the entropy of the universe.