Suppose you are recording a video of someone playing billiards. The balls crash into each other, and if you sit down and calculate the energy and momentum of the balls before and after a collision you will find that energy is conserved and momentum is conserved in each collision. Now, if you reverse the video, you will see the collision going backward, and if you do the same calculation, energy and momentum are still conserved. Just by seeing the video of a given collision, you have no way of knowing which way time is flowing. This is called time-reversal invariance, and Newton's laws of mechanics demand it.
Now let's go back to the example of putting an ice cube in a cup of hot coffee. Heat flows out of the coffee and into the ice until it all melts. This follows energy conservation, the first law of thermo, and the second law.
But what of the reverse time situation? Does the liquid in a coffee cup spontaneously heat up while forming an ice cube? No! That cannot happen: the second law specifically says the heat flows from hot to cold. But energy and momentum would be conserved in that process, so why doesn't it ever happen?
This is a paradox, seemingly. Mechanics says that running a video backwards you see something that obeys the laws of physics. But if you run the film of the ice in the coffee backwards, now you can tell which direction time flows, since when the ice cube spontaneously forms, something is very wrong. The 2nd law contradicts Newton's Laws!
This leads me to something I must point out: the second law is not a rigorous law of nature. All rigorous laws obey time reversal symmetry. But heat only flowing from hot to cold is not time invariant. In principle, if you waited long enough, the occasion of the ice cube spontaneously forming would happen. You would, for reasons I discuss later, have to wait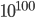 
years or so! So, what we should say is that heat flows from hot to cold almost always. The occasions where this does not happen for a macroscopic (regular size) object are so rare that in the entire time the universe has existed, it has probably never happened.
The thing that determines how long you have to wait for an "irreversible" process to reverse itself depends on how many particles there are in the process. Suppose you have two bottles, one of which is empty (no molecules in it at all) and the other which has some molecules in it. If you put the bottles together, the gas flows to fill both of them, which is irreversible. If you watched a video of it backwards it would look very weird. But what if the bottle that had gas at the beginning had only one single atom? Then it wouldn't take very long at all for the situation to reverse itself. You just have to wait for that atom to bounce back into the original bottle it was in. If you had two molecules, it also wouldn't take long for the situation to reverse itself.
Let's do a little calculation, since this will segue into further topics. Once the gas molecules flow into the second bottle, how long would it take before the process was likely to reverse itself?
If we have just one atom, and we assume that molecules can rearrange themselves every 1 trillionth of a second (called a femtosecond or fs), it wouldn't take long at all. The molecule has a 50/50 chance of being in the container it came from. So within 2 fs it will likely have reversed itself. Now say there were two molecules. Call the original full container A and the other one B. Then the following arrangements can occur:
- Both in A container (the situation where the process reversed itself)
- Molecule 1 in A and molecule 2 in B
- Molecule 2 in A and molecule 1 in B
- Both in container B
So there are 4 possibilities, and 1 out of 4 is the one that reversed the irreversibility, meaning that if you waited 4 fs, you'd be likely to see it happen.
Obviously, we could keep going. Three molecules would have 6 possibilities, four would have 24 possibilities, etc. The numbers are getting big fast! Five molecules would have 120 possibilities, with only 1 of them being the situation where all the gas molecules spontaneously went back to their bottle. The total number of possibilities, as you may know is 
, where the exclamation point is "factorial", and means that you multiply 
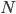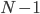times 
times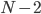 
,etc., until you get down to 1. So 5! is 5*4*3*2*1. The probability of the situation reversing itself spontaneously is 1 divided by . Now, when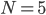 
, that's not too bad; you only have to wait 120 fs before the situation probably would happen. But on a real-world scale, 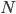equals 100,000,000,000,000,000,000,000. Can you imagine how large is in that case?! Your calculator will probably not even be able to compute it. (Mine insists that this number is infinity!) If you want an actual figure, I can only express it in an exponent: it's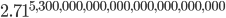 
. And the probability of finding all the gas back where it was is 1 divided by that number. Can it reverse itself spontaneously? Well, you'd have to wait that many femtoseconds, and the universe has only been around for 
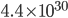femtoseconds. So ... no.
Now, of course, you, an outside agent, can reverse it. You can set up a pump between the two bottles, and force the atoms back into the first one. But in that case you have to do some work. It will never spontaneously reverse itself. And this is also true of coffee spontaneously boiling and forming an ice cube. It could happen. But the odds against it are literally so low that they're not even calculable by me. In the most optimistic view of how long the universe will exist, it would never happen.
We'll come back to this shortly, but the bottom line is that the 2nd law implies that time goes in one direction. In addition to heat flowing from hot to cold, irreversible things like mixing or releasing a gas into another bottle don't undo themselves, at least when they involve a realistic number (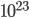
) particles, like they do in real life.