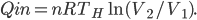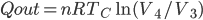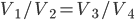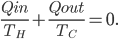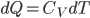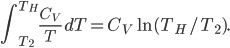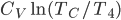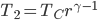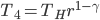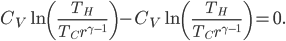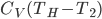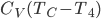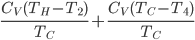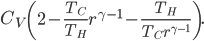When we're talking thermo, we're talking about systems. A system could be the gas in a room, a chunk of metal, a beaker full of water---anything with a bunch of atoms. A system has volume, pressure, temperature, and internal energy. But, since we've started running into a problem with reversibility, you might start to wonder whether there's something important missing from this list.
Let's look at the Carnot cycle and the Otto cycle side-by-side:
| Carnot Cycle | Otto Cycle | |
| Step 1 | Compression from 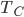 to to 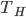 |
Compression from 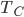 to to 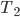 |
| Step 2 | Heating while expanding and doing work. Temperature is the same throughout. |
Heating from 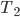 to to 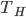 by byabsorbing heat. |
| Step 3 | Expanding while doing work and cooling from 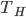 to to 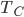 |
Expansion while doing work and cooling from 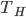 to to 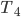 |
| Step 4 | Compress gas while exhausting heat. Temperature remains the same throughout. |
Cool gas from 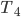 to to 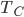 by byexhausting heat. |
Can you spot the difference?
The difference is when we're adding or subtracting heat in the Otto cycle, we let the temperature change. We never do that in the Carnot engine. And since heat only flows from hot to cold, these two steps (2 and 4) are irreversible. If you ran the film backwards, the air in the piston would dump a bunch of its heat into the hot bath to reduce its temperature, which never happens according to the 2nd law (heat flows from hot to cold). At the same time, while we were heating we lost the opportunity to do work. So, what we're looking for is a quantity that only shows up when we missed that opportunity. Let's see if we can quantify "lost opportunity to do work", or irreversibility. The quantity we're looking for will be zero for the Carnot engine, and nonzero for the Otto engine.
We're going to look at heat divided by temperature. That is, for some stage of a process, we'll take the heat added and divide that by the temperature it was added at. This is a simple thing to do. For the Carnot engine, the compression in step 1 has no heat added or subtracted. Step 3 also has no heat. In Step 2 the temperature stays the same, and some heat is added. In step 4 the temperature stays the same and heat is thrown out.
The sum of "heat added divided by temperature" is zero for the cycle.
Whatever heat divided by temperature is, if you add all of them up for a Carnot cycle, you get zero. Now, that's for the engine. But suppose we want to ask what the heat divided by temperature is for the entire universe. That is also zero! So, the Carnot engine does not change heat divided by temperature for the entire universe. It's zero. This reflects the fact that no opportunity to do work was lost, and that whatever we did can be undone. (In this case, we just put the work done back in, and all the heat will be put back where it was. The Carnot engine is reversible, so it can always be run as a refrigerator if we run it backwards by putting work into it.)
Now let's look at the same thing for the Otto cycle. Again, Steps 1 and 3 have no heat, so 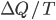 is zero. In stages 2 and 4, the heat can be calculated for the engine.
is zero. In stages 2 and 4, the heat can be calculated for the engine.
Just like for the Carnot engine, the total of heat over temperature for the Otto engine is zero. That's very interesting, because it means that just like temperature, volume, pressure, and internal energy, heat over temperature has no overall change for a cycle. So maybe whatever heat over temperature is also is a property of the system.
Now, for the Otto cycle, we should also check what heat over temperature is for the universe.
The change in heat over temperature is not zero for the Otto cycle! According to what I've been saying, that's because the Otto cycle is one that misses an opportunity to do work. And since the engine is not reversible, we cannot go back: that opportunity is lost forever. And that's reflected in the change in heat over temperature.
Let's go ahead and give "change in heat over temperature" a name: it's the change in entropy. The entropy of a system, always denoted by 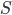 , is something that depends on its temperature, pressure, volume, etc. For an engine, just like all the other variables I mentioned,
, is something that depends on its temperature, pressure, volume, etc. For an engine, just like all the other variables I mentioned, 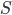 must be reset at the end of the cycle. And, if there is ever a change in
must be reset at the end of the cycle. And, if there is ever a change in 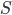 for the universe, that represents that somebody did something irreversible, and that they didn't do the maximum possible work. From then on, nobody will ever be able to undo that act: the total entropy of the universe is a big number, and when you increase it, it never decreases again.
for the universe, that represents that somebody did something irreversible, and that they didn't do the maximum possible work. From then on, nobody will ever be able to undo that act: the total entropy of the universe is a big number, and when you increase it, it never decreases again.