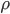Last time I discussed the fact that the atmosphere's pressure goes down as you go up in altitude. This was because a certain amount of air is compressed by the weight of all the air above it, so the higher you go up, the less squished the gas is, and so the pressure is lower. But to actually estimate what the pressure was, I had to assume that the temperature was the same at every altitude, and everybody knows that's wrong. So, we want to ask why it's colder in the mountains, and how much colder it is.
First, from a basic physics standpoint, it kind of makes sense. The molecules at higher altitudes had to give up some of their energy in order to get up there. So, it may be intuitively natural that they are going slowly, and that their temperature is low.
But there's also the fact that the pressure is lower up there because of the weight of air above it, and so if a volume of air rises, it also expands. We know that if a quantity of gas expands, it will cool down (unless someone adds heat). That's the First Law, that internal energy decreases if work is done and there's no heat: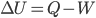 
with 
.
Let's focus on a given amount of air at an altitude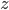 
. If it rises without being heated, then the first law days that 
, and 
. The change in internal energy,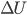 
, is the heat capacity (at constant volume) times the change in temperature. So
We just need to relate these quantities to each other, knowing what we know about gases.
Important!
The ideal gas law says that
and we could take a differential
is constant since we're talking about a given quantity of atoms. We can put this into the above equation,
or using the ideal gas law again,
Rearrange this and divide by
,
We already know
, thankfully. It was given in the last section that
Thus,
is the density of air, which is its mass divided by its volume. So
For argument's sake, let's talk about 1 mole of dry air. The heat capacity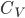 
divided by mass 
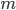is called the specific heat capacity. It's about 717 joules per kg to raise the temperature by 1 K. 
is the number divided by the mass for 1 mole (since we are talking about 1 mole, that's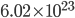 
), times Boltzmann's constant, which works out to 286.8 J per kg per Kelvin. Thus the total denominator is very close to 1000 J/K. That means that the change in temperature with height is 0.0098 Kelvin per meter, or 9.8 K per kilometer. Since Celsius is the same as Kelvin, that's 9.8 C/kilometer.
Translated into English units, that's a drop of 28.4° Fahrenheit for every mile you go up.
This figure, 28.4° F/mile is called the dry adiabatic lapse rate. It's called this because we did not factor in the effect of water vapor on the heat capacity, and because we assumed that the atmosphere didn't heat or cool the gas by conduction while it rose. If you factor those other things in, you get the moist adiabatic lapse rate, which is more like 14° F/mile. So, we might expect that on average, Denver is between about 14 and 25 degrees colder than at sea level. This depends on the relative humidity and how well the atmosphere is mixing at any given time, but it's a decent estimate.