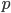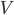Thermo for normals (part 11): Storing heat

Why is it that the cheesy part of a pizza can burn your mouth, but the crust doesn't? They both came out of the same oven, at the same temperature, but it seems like the cheese has more "heat" (actually internal energy 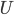) stored inside of it. When you put it in your mouth, it heats your mouth until it and your mouth reach the same temperature. But while the crust seems to give up all its heat quickly, and without having to throw off very much heat, the cheese seems to throw off a ton of heat in order to reach your mouth's temperature.

Thermal internal energy 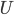, is the energy inside something that is in the kinetic and potential energy of the atoms that make it up. There must be some relationship between 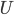and the temperature . But what is that relationship? Is it the same for all substances? What do you think?

The heat capacity is the amount of heat you need to add to something in order to make the temperature increase by 1 degree. It takes 1 calorie to make 1 cubic centimeter of water rise by 1 Kelvin. (That's just the definition of a calorie.) For 1 cubic centimeter of air, the amount of heat you have to add to go up 1 Kelvin is only around 0.0004 calories. So water has more than 2500 times more heat capacity for the same volume! Metals like aluminum have a heat capacity somewhere in between water and air, at about 0.5 calories to make a cubic centimeter go up 1 degree.

Suppose the power goes out, and you're worried about the tiramisu you have in the refrigerator spoiling. If the fridge has nothing in it but your dessert and air, you have a problem. Heat will start leaking in, and will easily increase the temperature of the air. This heat will then all go directly into your dessert. But if you have a bunch of water bottles in there, all at low temperature, you're much safer. It will take a long while before the heat leaking in can appreciably increase the temperature of  the water.

What might be obvious from this discussion is that if you have a substance of some volume, the more particles you have in that volume the better, for storing heat anyway. Gases are diffuse, so 1 cubic centimeter (at standard pressure) isn't very many atoms. Water and metal are dense, so there's a lot of atoms per volume. This makes sense. If the temperature is the average energy per particle, then adding a fixed amount of heat (like 1 calorie) is going to give you varying amounts of temperature increase. For gas, the heat is divided among relatively few atoms, so each gets a large share and the temperature rises a lot. In dense materials the energy gets divided among lots of atoms, so there's a small temperature change, as each atom gets a small portion.

This is not to say that the heat capacities for all gases are the same. Some gases are better at stuffing heat into themselves than others. When a gas absorbs heat, since there is no potential energy between gas atoms, a given molecule has to put the heat into either kinetic energy, or potential energy within the molecule by the stretching of the chemical bond. But some gases have more kinds of kinetic energy than others. Moving along a certain direction is one way of having kinetic energy, but rotations and tumbling is another way. If a gas is monatomic, meaning that the atoms in the gas aren't bonded to each other, then the gas only has 3 ways of moving, one for each dimension it can travel along (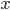, , 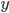and 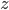). It can't tumble because it's just a point. This would include things like argon, neon, and xenon. But lots of gases, like the air, are made up of diatomic molecules, where the atoms pair up to make barbell shaped molecules (such as O₂ and N₂). These gases then have three extra ways of storing energy, and thus three extra ways to stuff energy into themselves: they can rotate along two axes, and they can put energy into stretching of the bond between them. As such, they have a higher capacity for holding heat. If that's so, then oxygen gas (which is diatomic) should have double the heat capacity of argon gas (which is monatomic). Is that true? Yes!

If we think of it that way, then all solids should have the same heat capacity. Solids have 6 ways to divide energy up, 3 kinetic and 3 potential. There's no tumbling nonsense like above, just a bunch of atoms held in a 3D crystal as if by little springs to each other. So, speaking of metals specifically (and almost all species on the periodic table are metals), they should all have the same heat capacity per particle (or per mole), and it should be roughly the same as air (per molecule! Not for the same volume, for the same number of molecules). And it's true! The heat capacities for most metals are about 6 calories per degree C for every mole, within 15% of air (6.9 calories per C per mole). This is called the law of Dulong and Petit.

Now, water is a whole other story. Unlike gases, it has potential energy. And unlike solids, it has tumbling in addition to this potential energy. And it has two molecular bonds to store energy in. So, water can store a ton of heat without going up in temperature very much. If you microwave a burrito, the plate can get very hot while the burrito is lukewarm. Why? Water! You put the same amount of heat into both the plate and the burrito, but the temperature of the plate went up much faster because it doesn't have as many ways to stuff heat into itself (i.e. it has a low heat capacity). The burrito, by having water in it, has tons of ways to store heat (i.e. it has a high heat capacity). So the temperature of the burrito goes up very little compared to the plate.